
[의학 생명] 수학 세특 주제 탐구
삼각함수가 활용된 호흡주기 분석
안녕하세요. 대치동 미래인재컨설팅입니다. 인간의 호흡은 생명 유지에 필수적인 생리적 과정으로, 심박수와 함께 건강 상태를 평가하는 중요한 지표로 사용됩니다. 이러한 호흡 주기를 분석하면 폐 기능, 호흡 패턴 및 관련 질환을 진단할 수 있습니다. 이는 호흡기 질환의 조기 발견과 관리에 중요한 역할을 합니다.
호흡 주기를 분석하는 여러 방법 중 삼각함수를 사용하는 접근법은 특히 주목할 만한 장점을 제공합니다. 삼각함수는 반복적인 패턴과 파형을 갖는 데이터를 분석하는 데 유용하며, 주기적인 호흡 특성을 정확하게 모델링할 수 있습니다. 이 블로그 포스팅에서는 삼각함수가 호흡 주기 분석에 어떻게 활용될 수 있는지, 그리고 이를 통해 얻을 수 있는 다양한 통찰력에 대해 알아보겠습니다.
삼각함수는 특히 호흡 주기의 반복성과 진폭 변화를 수학적으로 나타내고 분석하는 데 효과적입니다. 이런 수학적 접근법을 통해 호흡 패턴을 정량화하고, 이상 징후를 감지하며, 개인 맞춤형 건강 관리 전략을 제시할 수 있습니다. 오늘 대치동 미래인재컨설팅에서는 삼각함수가 호흡 주기 분석에 어떻게 적용되는지 구체적으로 살펴보도록 하겠습니다.
삼각함수의 기본 개념
삼각함수는 삼각형의 각도와 변의 길이 사이의 관계를 수학적으로 표현하는 함수입니다. 삼각함수는 주로 직각삼각형에서 각도와 변의 비율을 통해 정의되며, 주기적이고 반복적인 특성을 갖습니다.
1. 사인 함수
직각삼각형에서, 한 각의 사인은 그 각에 대한 대변의 길이를 빗변의 길이로 나눈 값입니다.

사인 함수는 주기가 2π인 주기 함수입니다. 즉, sin(θ+2π)=sin(θ)입니다.
2. 코사인 함수
직각삼각형에서, 한 각의 코사인은 그 각에 대한 인접변의 길이를 빗변의 길이로 나눈 값입니다.

코사인 함수도 주기가 2π인 주기 함수입니다. 즉, cos(θ+2π)=cos(θ)입니다.
3. 탄젠트 함수
직각삼각형에서, 한 각의 탄젠트는 그 각에 대한 대변의 길이를 인접변의 길이로 나눈 값입니다.

탄젠트 함수는 주기가 π인 주기 함수입니다. 즉, tan(θ+π)=tan(θ)입니다.

호흡주기 모델링

1. 주기적 패턴 표현
호흡의 주기적 패턴을 모델링하기 위해 가장 일반적으로 사용되는 수식은 사인(sin) 함수입니다. 사인 함수는 다음과 같은 형태를 가집니다.
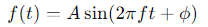

2. 주기와 진폭 조절
호흡의 주기와 진폭을 조절하는 데 사용되는 수식은 다음과 같습니다.
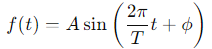
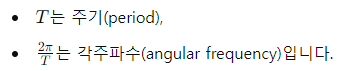
3. 위상 이동 표현
호흡의 시작 시점을 조정하기 위해 위상 이동을 포함할 수 있습니다. 위상 이동을 적용한 수식은 다음과 같습니다.
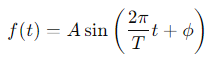
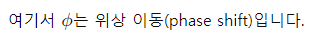
4. 합성 곡선 생성
여러 개의 삼각함수를 합성하여 복잡한 패턴을 생성할 수 있습니다. 예를 들어, 두 개의 사인 함수를 합성할 수 있습니다.
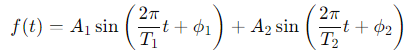

5. 신호 처리와 분석
신호 분석을 위해 푸리에 변환(Fourier Transform)을 사용합니다. 시간 영역의 신호 f(t)f(t)를 주파수 영역으로 변환하는 수식은 다음과 같습니다.
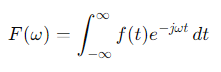

각 전공 계열에서 삼각함수가 활용된 호흡주기 분석의 관심사와 적용 방향이 다양하게 나타납니다. 따라서 학생들은 자신의 관심과 탐구 목표에 따라 다양한 주제를 선택할 수 있습니다. 대치동 미래인재 입시컨설팅에서는 학생들이 의학 생명 계열 진로를 향해 나아가기 위해 수학 및 미적분 교과와 관련된 세특 보고서, 주제 탐구 보고서, 수행평가 결과물, 동아리 활동 보고서, 그리고 진로 활동 보고서 등을 통합적으로 다루며, 이를 기반으로 한 1:1 컨설팅을 통해 학생들의 학습 및 진로 계획을 지원하고 있습니다.
대치동 미래인재 입시컨설팅은 무료 컨설팅을 제공하며, 지역별 입시 설명회도 주최하고 있습니다. 관심 있는 학생과 학부모님은 아래 대치동 미래인재 입시컨설팅 이벤트 배너를 클릭하여 신청하시기 바랍니다. 우리아이의 대입 성공을 위해 최고의 입시 파트너를 찾아보세요 ^^!

'세특 자료' 카테고리의 다른 글
| [의학 생명] 통합과학 세특 주제 탐구 - 생명 시스템의 기본 단위에 대한 연구 (0) | 2024.07.31 |
|---|---|
| [경영 경제] 확률과 통계 세특 주제 탐구 - 확률 변수가 활용된 경제 예측 (0) | 2024.07.31 |
| [의학 생명] 미적분 세특 주제 탐구 - 삼각함수의 적분이 활용된 근전도(EMG) 분석 (0) | 2024.07.30 |
| [의학 생명] 확률과 통계 세특 주제 탐구 - 확률 변수가 활용된 의료 빅데이터 분석 (0) | 2024.07.30 |
| [과학 공학] 수학 세특 주제 탐구 - 삼차 방정식이 활용된 기계 로봇 공학 (0) | 2024.07.27 |