미래인재컨설팅학원

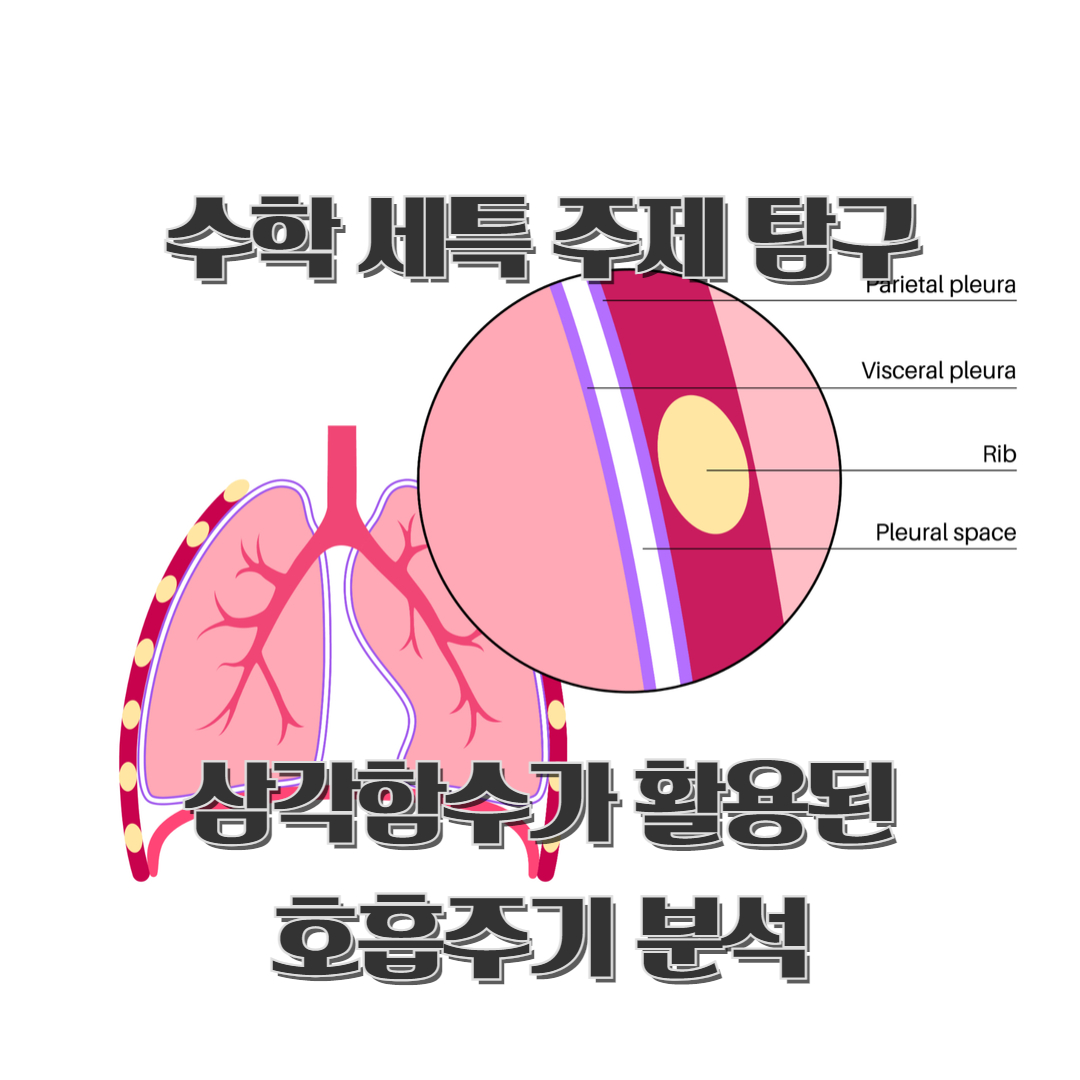
[의학 생명] 수학 세특 주제 탐구삼각함수가 활용된 호흡주기 분석 안녕하세요. 대치동 미래인재컨설팅입니다. 인간의 호흡은 생명 유지에 필수적인 생리적 과정으로, 심박수와 함께 건강 상태를 평가하는 중요한 지표로 사용됩니다. 이러한 호흡 주기를 분석하면 폐 기능, 호흡 패턴 및 관련 질환을 진단할 수 있습니다. 이는 호흡기 질환의 조기 발견과 관리에 중요한 역할을 합니다.호흡 주기를 분석하는 여러 방법 중 삼각함수를 사용하는 접근법은 특히 주목할 만한 장점을 제공합니다. 삼각함수는 반복적인 패턴과 파형을 갖는 데이터를 분석하는 데 유용하며, 주기적인 호흡 특성을 정확하게 모델링할 수 있습니다. 이 블로그 포스팅에서는 삼각함수가 호흡 주기 분석에 어떻게 활용될 수 있는지, 그리고 이를 통해 얻을 수 있는 다..

[의학 생명] 미적분 세특 주제 탐구삼각함수의 적분이 활용된 근전도(EMG) 분석 안녕하세요. 대치동 미래인재컨설팅입니다. 근전도(EMG, Electromyography)는 근육의 전기적 활동을 기록하고 분석하는 생리학적 기술로, 근육 기능을 평가하고 신경계와 근육계 간의 상호작용을 연구하는 데 필수적인 도구입니다. EMG 신호는 복잡한 생체 전기 신호로, 이를 정확히 분석하고 해석하기 위해서는 다양한 수학적 기법이 필요합니다. 특히, 삼각함수와 그 적분은 EMG 신호의 주기적 특성을 이해하고 처리하는 데 중요한 역할을 합니다. 삼각함수는 주기적인 특성을 가지고 있어, 주기적으로 변하는 EMG 신호를 분석하는 데 효과적으로 활용됩니다. EMG 신호는 주로 주파수 도메인에서 분석되며, 이때 푸리에 변환과 ..

[의학 생명] 확률과 통계 세특 주제 탐구확률 변수가 활용된 의료 빅데이터 분석 안녕하세요. 대치동 미래인재컨설팅입니다. 의료 분야에서는 환자의 건강 상태를 정확하게 진단하고 효과적으로 치료하는 것이 매우 중요합니다. 이 과정에서 높은 정확성과 신뢰성이 요구됩니다. 이에 따라, 대규모 데이터를 처리하고 분석할 수 있는 기술의 중요성이 점점 커지고 있습니다. 최근 몇 년 동안 의료 빅데이터는 의료 산업의 혁신을 이끄는 핵심 요소로 부상했으며, 다양한 데이터 소스로부터 얻은 정보를 활용해 의료 서비스의 질을 향상시키고 비용 절감에 기여하고 있습니다.이러한 빅데이터 분석의 중심에는 '확률 변수'라는 중요한 개념이 있습니다.확률 변수는 통계와 데이터 분석에서 불확실성을 모델링하고 예측하는 데 사용하는 기본적인 ..

[과학 공학] 수학 세특 주제 탐구삼차 방정식이 활용된 기계 로봇 공학 안녕하세요. 대치동 미래인재컨설팅입니다. 기계 로봇 공학은 혁신적인 기술 발전과 더불어 눈부신 성장을 이루고 있습니다. 이 분야에서 로봇의 동작을 제어하고 최적화하려면 수학적 모델링이 반드시 필요합니다. 특히 삼차 방정식은 로봇의 운동학 및 동역학을 이해하고 제어하는 데 핵심적인 역할을 합니다. 삼차 방정식은 복잡한 운동 패턴을 설명하고, 로봇 관절의 움직임을 정확히 예측하며, 시스템의 안정성을 평가하는 데 활용됩니다. 이번 대치동 미래인재컨설팅의 포스팅에서는 삼차 방정식이 기계 로봇 공학에 어떻게 활용되는지 살펴보도록 하겠습니다. 이를 통해 로봇 공학의 깊이 있는 이론적 기반과 실질적인 응용 가능성을 더욱 명확히 이해할 수 있을 것..

[의학 생명] 생명과학 세특 주제 탐구후성 유전학이 활용된 암치료 안녕하세요. 대치동 미래인재컨설팅입니다. 최근 몇 년 동안의 연구와 혁신을 통해 암 치료에서 후성 유전학의 중요성이 점점 더 부각되고 있습니다. 후성 유전학은 유전자 서열의 변형 없이 유전자 발현을 조절하는 메커니즘을 연구하는 분야로, 암의 발생 및 진행과 밀접한 관련이 있습니다. 암세포는 정상세포와 달리 후성 유전적 변화를 통해 세포 분열 및 성장을 비정상적으로 조절합니다. 이러한 변화는 DNA 메틸화, 히스톤 변형, 비암호화 RNA 등 여러 가지 후성 유전적 메커니즘을 포함합니다. 최근 연구들은 후성 유전적 변화를 표적으로 삼아 암세포의 성장을 억제하고, 기존의 암 치료법에 대한 저항을 극복할 수 있는 새로운 치료법 개발에 집중하고 있..

[의학 생명] 통합과학 세특 주제 탐구화학반응이 적용된 뇌신경과학 안녕하세요. 대치동 미래인재컨설팅입니다. 뇌신경과학(Neuroscience)은 인간의 두뇌와 신경계의 구조 및 기능을 탐구하고 이해하는 학문입니다. 이 분야는 신경 세포(뉴런) 간의 상호작용, 신경 회로의 구조, 그리고 이러한 요소들이 우리의 사고, 감정, 행동을 어떻게 형성하는지에 대해 연구합니다. 이러한 연구는 주로 전기적 신호 전달과 신경화학적 반응을 통해 이루어집니다. 특히, 신경화학은 뉴런 간의 소통을 가능하게 하는 화학 물질인 신경전달물질과 이로 인해 발생하는 다양한 생화학적 반응을 연구합니다. 신경전달물질은 뉴런이 시냅스라는 접합 부위를 통해 신호를 전달하는 데 핵심적인 역할을 합니다. 이러한 신호 전달 과정은 다양한 화학 반..

[과학 공학] 기하 세특 주제 탐구공간벡터가 활용된 우주 항공 및 우주 탐사 안녕하세요. 대치동 미래인재컨설팅입니다. 우주 항공과 탐사는 인류의 호기심과 도전 정신의 결정체입니다. 우리는 지구의 한계를 넘어 우주의 비밀을 밝혀내고 새로운 프론티어를 개척하기 위해 끊임없이 노력해 왔습니다. 이러한 노력을 성공으로 이끌기 위해서는 다양한 과학적 도구와 기술적 방법론이 필요합니다.공간벡터는 위치와 방향을 나타내는 단순한 수학적 개념을 넘어서, 우주에서의 이동과 위치 결정에 중요한 역할을 합니다. 예를 들어, 로켓의 궤적을 정확히 계산하거나 인공위성의 안정적인 궤도 유지를 위해서는 공간벡터에 대한 정확한 이해와 적용이 필수적입니다. 우주 탐사선이 특정 행성이나 소행성에 접근하고 착륙하는 절차에서도 공간벡터는 중..

[의학 생명] 미적분 세특 주제 탐구삼각함수의 미분이 활용된 운동 생리학 연구 안녕하세요. 대치동 미래인재컨설팅입니다. 운동 생리학 연구는 인체의 기능과 성능을 분석하고 이해하기 위해 다양한 수학적 기법을 사용합니다. 그 중에서도 삼각함수와 미분은 특히 중요한 역할을 합니다. 삼각함수는 주기적이고 반복적인 운동 패턴을 설명하는 데 효과적이며, 이를 미분함으로써 운동의 변화율과 동적 특성을 더 정밀하게 분석할 수 있습니다. 예를 들어, 심박수, 호흡 패턴, 근육의 수축과 이완 과정 등과 같은 생리적 현상들은 삼각함수를 이용해 모델링할 수 있습니다. 이러한 모델링은 운동 성과를 최적화하고, 부상 예방 및 재활 과정에 중요한 인사이트를 제공합니다.대치동 미래인재컨설팅에서는 삼각함수의 미분이 운동 생리학 연구에..

[과학 공학] 확률과 통계 세특 주제 탐구확률변수가 활용된 신소재 개발 안녕하세요. 대치동 미래인재컨설팅입니다. 21세기 들어 첨단 기술이 발전하면서 신소재 개발의 중요성이 더욱 강조되었습니다. 신소재는 기존의 한계를 넘어 새로운 기능을 구현할 수 있는 물질로서, 전자, 에너지, 생명공학 등 다양한 분야에서 혁신을 주도하고 있습니다. 이러한 신소재의 개발 과정은 매우 복잡하고 여러 단계를 거치며, 다양한 변수가 관여합니다. 이때 확률변수는 신소재의 특성을 예측하고 최적화하는 데 중요한 역할을 합니다. 확률변수는 통계학에서 어떤 실험이나 관찰의 가능한 결과를 수치로 표현한 것을 의미합니다. 이는 신소재 개발 과정 중 발생할 수 있는 여러 변화를 수치적으로 모델링하고 분석하는 것이 중요합니다. 예를 들어, ..

[의학 생명] 수학 세특 주제 탐구로그함수가 활용된 생물 통계학 안녕하세요. 대치동 미래인재컨설팅입니다. 생물 통계학은 생물학적 데이터를 수집하고, 이를 분석 및 해석하는 과학적 방법을 연구하는 학문입니다. 이 분야는 유전자 연구, 생태계 평가, 임상 시험 등 다양한 생물학적 연구에서 중요한 역할을 합니다. 이러한 분석 과정에서 로그함수는 특히 중요한 도구로 사용됩니다. 로그 함수는 데이터의 분포를 더 정규에 가깝게 만들고, 광범위한 데이터를 처리하기 용이하게 하며, 상관관계를 더욱 분명하게 드러내는 데 효과적입니다. 로그 함수는 복잡한 데이터 세트를 간소화하여 분석의 효율성을 증대시키는 데 자주 활용됩니다. 예를 들어, 생물학적 데이터는 종종 비대칭적이거나 극단값이 많아 정규분포를 벗어나는 경우가 흔합..