미래인재컨설팅학원

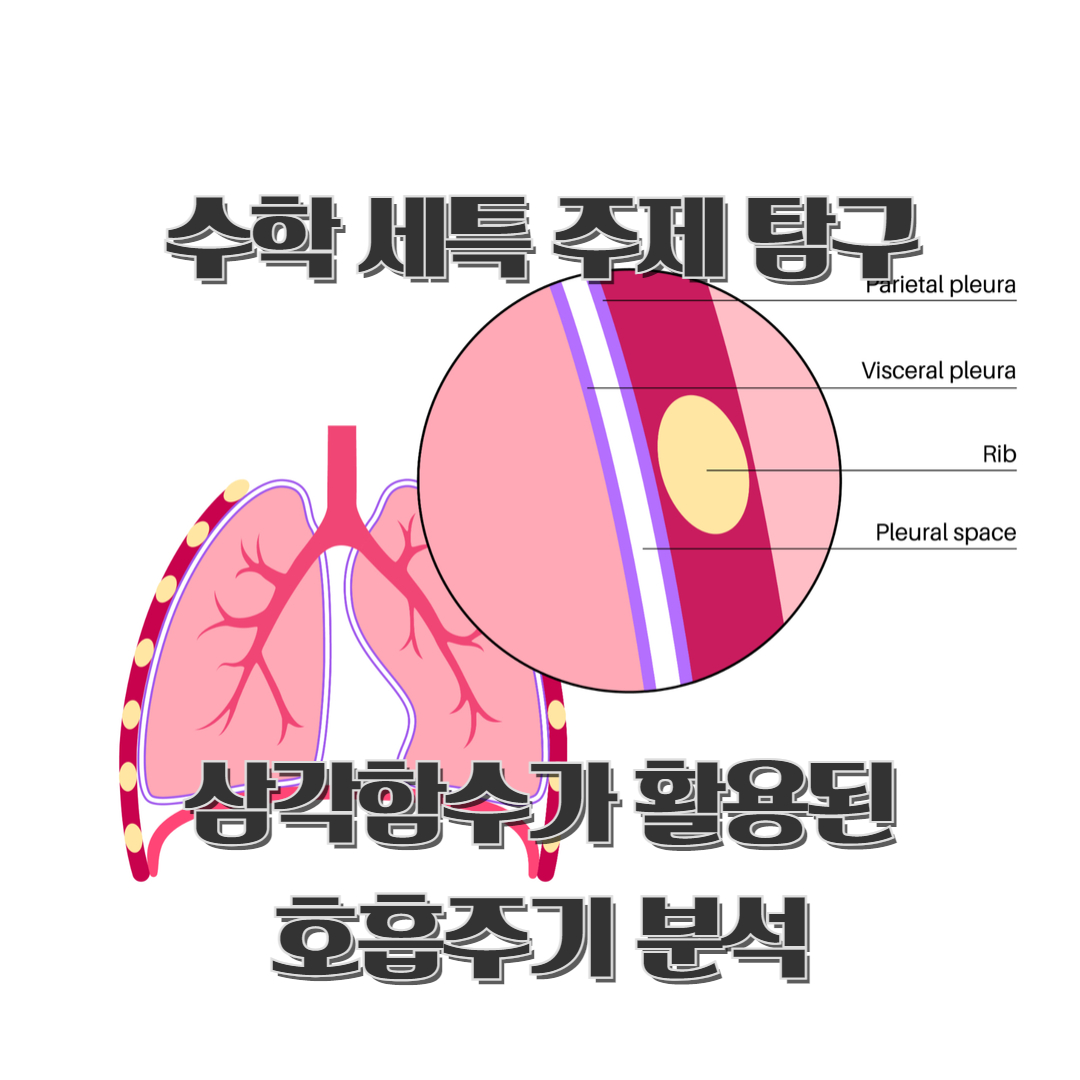
[의학 생명] 수학 세특 주제 탐구여러 가지 함수가 활용된 생명과학 안녕하세요. 대치동 미래인재컨설팅입니다. 생명과학은 생명체의 구조와 기능, 성장 과정, 기원, 진화, 그리고 분포를 탐구하는 학문으로, 지속적인 혁신과 발전이 이루어지고 있는 분야입니다. 이러한 발전의 핵심에는 복잡한 데이터를 분석하고 유의미한 정보를 도출하기 위한 다양한 함수들이 자리하고 있습니다. 유전자 서열 분석, 단백질 구조 예측, 질병 모델링 등에서 사용되는 함수들은 연구자들이 복잡한 생물학적 현상을 파악하고 새로운 발견을 이루는 데 중요한 역할을 합니다.이번 대치동 미래인재컨설팅 포스팅에서는 생명과학에서 사용되는 주요 함수들과 그들의 역할을 살펴보고자 합니다. 각 함수는 특정 생물학적 데이터를 처리하고 분석하는 데 활용되며, ..

[경영 경제] 수학 세특 주제 탐구삼각함수가 활용된 경제학 안녕하세요. 대치동 미래인재컨설팅입니다. 경제학은 인간 사회에서 일어나는 다양한 경제 활동과 현상을 분석하고 이해하는 학문입니다. 경제학자들은 다양한 수학적 도구와 방법론을 사용하여 복잡한 경제 현상을 설명하고 예측합니다. 특히 삼각함수는 주기적인 현상이나 변동을 분석하는 데에 유용한 도구로 널리 활용됩니다. 삼각함수는 기하학에서 유래된 개념으로, 각도와 이에 대응하는 삼각형 변의 길이 간의 관계를 다룹니다. 그러나 삼각함수의 특징, 특히 주기성과 파형을 분석하는 능력은 경제학에서도 중요한 응용 분야가 됩니다. 예를 들어, 삼각함수는 주기적인 경제 변수 분석, 계절적 변동 예측, 시장의 주기적 패턴 식별 등에 유용하게 사용됩니다. 이번 대치동 ..

[의학 생명] 수학 세특 주제 탐구삼각함수가 활용된 호르몬 분기 주기 분석 안녕하세요. 대치동 미래인재컨설팅입니다. 호르몬은 신체의 여러 기능을 조절하는 중요한 역할을 하는 화학 물질입니다. 특히 호르몬 분비 주기는 신체의 생리적 변화를 파악하고 건강을 유지하는 데 중요한 정보를 제공합니다. 이러한 호르몬 분비 주기는 주기적이며, 주기 패턴 분석에 삼각함수를 매우 유용하게 활용할 수 있습니다.삼각함수는 주기적인 현상을 수학적으로 표현하는 데 매우 효과적인 도구입니다. 사인(sine)과 코사인(cosine) 같은 삼각함수는 주기성을 지니기 때문에, 이를 사용해 시간에 따른 호르몬 분비 패턴을 정확하게 모델링하고 분석할 수 있습니다. 예를 들어, 생리 주기, 수면 주기, 스트레스 호르몬 분비 패턴 등 다양한..

[의학 생명] 수학 세특 주제 탐구삼각함수가 활용된 생체리듬 분석 안녕하세요. 대치동 미래인재컨설팅입니다. 현대 사회에서 건강과 웰빙에 대한 관심이 커지고 있습니다. 특히 생체리듬은 개인의 신체적, 정신적 상태를 이해하는 데 중요한 역할을 하고 있습니다. 생체리듬은 신체 내부에서 주기적으로 반복되는 다양한 생리적 변화를 의미하며, 이를 정확히 분석하고 이해하는 것은 건강 관리에 매우 유익합니다.생체리듬 분석에서 중요한 수학적 도구 중 하나는 삼각함수입니다. 삼각함수는 주기적인 변화를 수학적으로 표현하는 데 뛰어난 도구로, 고대부터 천문학과 항해 등 다양한 분야에서 사용되어 왔습니다. 대치동 미래인재컨설팅에서는 삼각함수가 생체리듬 분석에 어떻게 활용되는지 살펴보도록 하겠습니다. 이를 통해 신체 내부의 주기..

[의학 생명] 수학 세특 주제 탐구삼각함수가 활용된 호흡주기 분석 안녕하세요. 대치동 미래인재컨설팅입니다. 인간의 호흡은 생명 유지에 필수적인 생리적 과정으로, 심박수와 함께 건강 상태를 평가하는 중요한 지표로 사용됩니다. 이러한 호흡 주기를 분석하면 폐 기능, 호흡 패턴 및 관련 질환을 진단할 수 있습니다. 이는 호흡기 질환의 조기 발견과 관리에 중요한 역할을 합니다.호흡 주기를 분석하는 여러 방법 중 삼각함수를 사용하는 접근법은 특히 주목할 만한 장점을 제공합니다. 삼각함수는 반복적인 패턴과 파형을 갖는 데이터를 분석하는 데 유용하며, 주기적인 호흡 특성을 정확하게 모델링할 수 있습니다. 이 블로그 포스팅에서는 삼각함수가 호흡 주기 분석에 어떻게 활용될 수 있는지, 그리고 이를 통해 얻을 수 있는 다..

[과학 공학] 수학 세특 주제 탐구삼차 방정식이 활용된 기계 로봇 공학 안녕하세요. 대치동 미래인재컨설팅입니다. 기계 로봇 공학은 혁신적인 기술 발전과 더불어 눈부신 성장을 이루고 있습니다. 이 분야에서 로봇의 동작을 제어하고 최적화하려면 수학적 모델링이 반드시 필요합니다. 특히 삼차 방정식은 로봇의 운동학 및 동역학을 이해하고 제어하는 데 핵심적인 역할을 합니다. 삼차 방정식은 복잡한 운동 패턴을 설명하고, 로봇 관절의 움직임을 정확히 예측하며, 시스템의 안정성을 평가하는 데 활용됩니다. 이번 대치동 미래인재컨설팅의 포스팅에서는 삼차 방정식이 기계 로봇 공학에 어떻게 활용되는지 살펴보도록 하겠습니다. 이를 통해 로봇 공학의 깊이 있는 이론적 기반과 실질적인 응용 가능성을 더욱 명확히 이해할 수 있을 것..

[의학 생명] 수학 세특 주제 탐구로그함수가 활용된 생물 통계학 안녕하세요. 대치동 미래인재컨설팅입니다. 생물 통계학은 생물학적 데이터를 수집하고, 이를 분석 및 해석하는 과학적 방법을 연구하는 학문입니다. 이 분야는 유전자 연구, 생태계 평가, 임상 시험 등 다양한 생물학적 연구에서 중요한 역할을 합니다. 이러한 분석 과정에서 로그함수는 특히 중요한 도구로 사용됩니다. 로그 함수는 데이터의 분포를 더 정규에 가깝게 만들고, 광범위한 데이터를 처리하기 용이하게 하며, 상관관계를 더욱 분명하게 드러내는 데 효과적입니다. 로그 함수는 복잡한 데이터 세트를 간소화하여 분석의 효율성을 증대시키는 데 자주 활용됩니다. 예를 들어, 생물학적 데이터는 종종 비대칭적이거나 극단값이 많아 정규분포를 벗어나는 경우가 흔합..

[의학 생명] 수학 세특 주제 탐구합성 함수가 활용된 진단영상의학 안녕하세요. 대치동 미래인재컨설팅입니다. 진단영상의학은 현대 의학에서 굉장히 핵심적인 역할을 합니다. 환자의 내부 장기와 조직을 비침습적으로 시각화하여 질병 진단, 치료 계획 수립 및 경과 관찰에 필수적인 정보를 제공합니다. 이러한 진단 과정에서 사용되는 영상 기술에는 MRI, CT, 초음파 등이 있으며, 각각 고유한 특성과 장점을 지니고 있습니다. 하지만 이들 영상 기술이 제공하는 정보는 단일 모달리티로만 사용될 때에는 한계가 있을 수 있습니다. 예를 들어, CT는 높은 해상도의 구조적 정보를 제공하지만, 조직의 기능적 정보는 충분하지 않을 수 있습니다. 이러한 한계를 극복하기 위해 합성 함수가 진단영상의학 분야에 도입되었습니다. 합성 ..

[컴퓨터 SW] 수학 세특 주제 탐구지수함수의 원리가 활용된 컴퓨터 공학 안녕하세요. 대치동 미래인재컨설팅입니다. 컴퓨터 공학의 발전은 수학적 원리와 개념에 크게 의존하고 있으며, 특히 지수 함수는 여러 분야에서 중요한 역할을 합니다. 지수 함수는 단순한 형태에도 불구하고 알고리즘의 효율성 향상, 데이터 암호화, 기계 학습 모델링 등 다양한 분야에서 중요한 역할을 합니다.오늘 대치동 미래인재컨설팅의 포스팅에서는 지수 함수의 기본 개념을 이해한 후, 이를 컴퓨터 공학에서 어떻게 적용하는지 살펴보도록 하겠습니다.  알고리즘의 시간 복잡도1. 지수 시간 복잡도의 정의지수 시간 복잡도는 알고리즘의 실행 시간이 입력 크기 n에 대해 O(2^n) 또는 O(b^n) (여기서 b>1)으로 표현될 때를 말합니다. 이러한..

[컴퓨터 SW] 수학 세특 주제 탐구강화학습이 적용된 인공지능 연구 안녕하세요. 대치동 미래인재컨설팅입니다. 인공지능(AI) 연구는 다양한 분야에서 빠르게 발전하고 있는데, 그 중에서도 강화학습(Reinforcement Learning, RL)은 특히 주목받고 있는 기술입니다. 강화학습은 인간의 학습 원리를 모방하여 에이전트가 주어진 환경에서 상호작용하며 최상의 행동을 스스로 학습하는 기술입니다. 이 과정을 통해 에이전트는 다양한 상황에서 스스로 학습하고 적응하는 능력을 점차 향상시킵니다. 강화학습은 이러한 특성 덕분에 게임 인공지능(AI), 로보틱스, 자율주행, 그리고 추천 시스템 등 다양한 실제 응용 분야에서 높은 성과를 거두고 있습니다.오늘 대치동 미래인재컨설팅에서는 강화학습의 기본 개념, 작동 원..